¿Cómo adivinar el futuro en machine learning? - Primera parte

To forecast se puede traducir por predecir, normalmente tras un análisis de ciertos datos disponibles. En este sentido, todo el aprendizaje de máquinas podría ser considerado como forecasting, ya que su objetivo es predecir a través de modelos, el comportamiento de unos objetos de interés. Sin embargo, en machine learning se suele reservar el término forecasting para la predicción de series temporales, o time series forecasting.
¿Cómo se puede predecir una serie temporal?
Cuando disponemos de una serie de datos de una variable ordenados en el tiempo (ver Fig. 1) y deseamos predecir los siguientes valores que tomará esta serie temporal, lo ideal es conocer qué leyes rigen este comportamiento. Si bien para ciertos sistemas físicos o matemáticos es posible crear modelos que describan adecuadamente su comportamiento con los inputs correctos, aunque sea a corto plazo como puede ser el caso de la predicción del tiempo meteorológico (weather forecast), en general no se dispone de información sobre las leyes que rigen las series temporales que resultan de interés en machine learning. Debemos, por tanto, realizar ciertas hipótesis sobre la forma de la serie temporal para predecir su futuro.
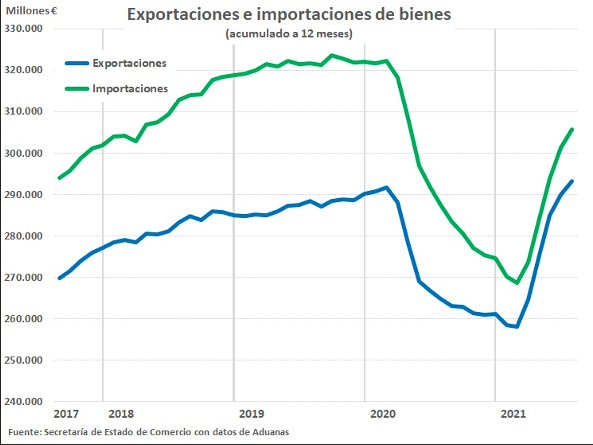
Conviene enfatizar que, al igual que en el resto de machine learning o en ciencia en general, no todo es predecible aunque usemos toda la información disponible. También es importante señalar que, cuanto más impredecible es un sistema, habitualmente los modelos simples son capaces de dar una predicción tan razonable como los sistemas complejos.
Algunos modelos simples
Existen varias maneras inmediatas de dar una predicción para una serie temporal. Con el modelo naïf o ingenuo (naïve model), asumimos que la serie mantendrá el valor de su última observación. Con el modelo deriva (drift), tomamos la variación media de la curva y suponemos que seguirá un crecimiento lineal dado por esta variación. Otra posible predicción es tomar la media de la serie temporal. Echa un vistazo a la Fig. 2.
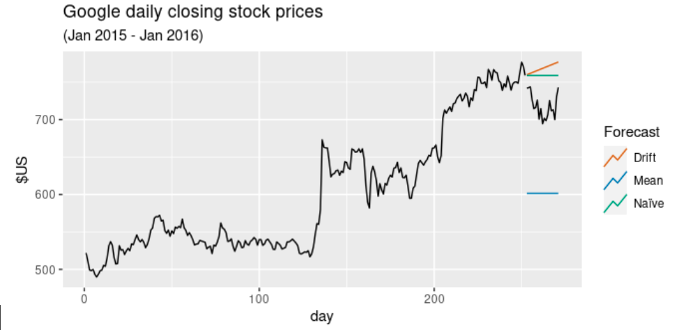
Descomposición de una serie temporal
Habitualmente, toda serie temporal que sea susceptible de ser predicha posee una tendencia (trend) y un número de estacionalidades(seasonalities).
- La tendencia indica el crecimiento de la curva en un momento dado.
- Las estacionalidades son curvas periódicas con un período que puede ser diario, semanal, mensual, anual…
Si la amplitud de la parte estacional es constante, podemos escribir la serie temporal como una suma de tendencia, estacionalidad o estacionalidades, y un término de resto que es impredecible, y que idealmente seguiría una distribución estadística controlada (gaussiana, por ejemplo)(mirar Fig. 3):
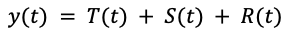
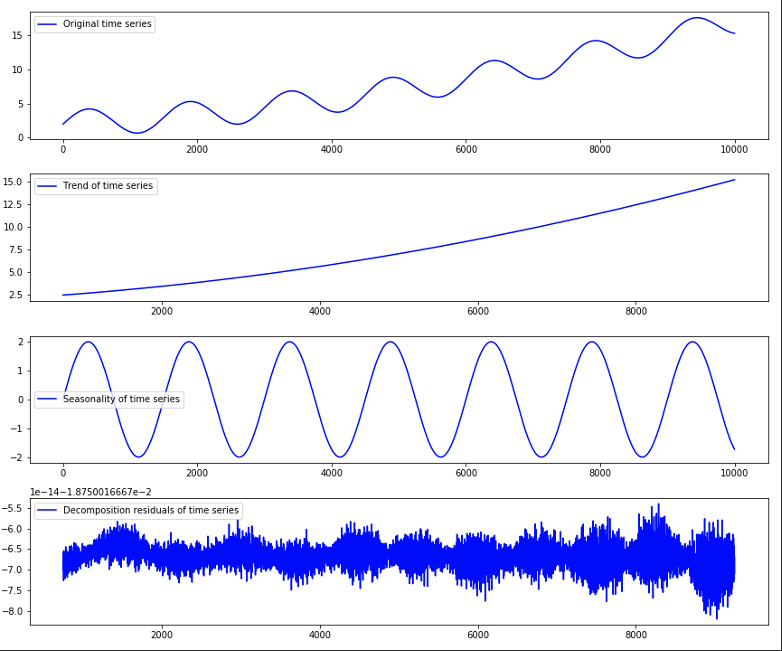
Sin embargo, otras series temporales pueden presentar una amplitud de la parte estacional que depende de su tendencia (ver Fig. 4). Para estas series temporales suele ser más adecuado usar un productorio de las tres componentes:
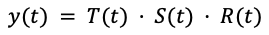
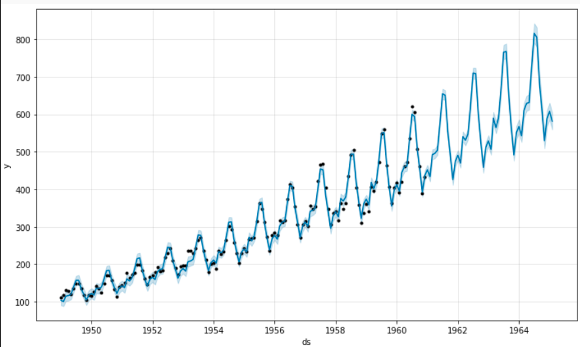
Esta división en tendencia y estacionalidades es muy útil tanto conceptual como prácticamente, pues hay modelos como el suavizado exponencial (exponential smoothing) o Prophet, que modelan estas componentes por separado.
Modelos autorregresivos
Los modelos autorregresivos parten de la hipótesis de que la serie temporal se puede describir a partir de una combinación lineal de valores pasados:
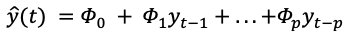
Los coeficientes Φ se pueden obtener de un ajuste o entrenamiento con datos reales. Por ejemplo, minimizando la función de suma de distancias al cuadrado:
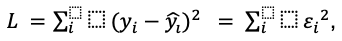
Donde representan yi los datos reales e ŷi las predicciones del modelo autorregresivo. Para un ejemplo práctico, échale un vistazo a este enlace.
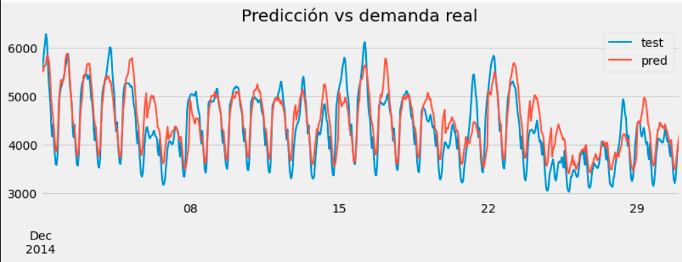
Modelos de media móvil
Los modelos de media móvil son similares a los autorregresivos, pero en vez de suponer una combinación lineal de los valores pasados, supone una combinación lineal de los errores del modelo que sirva de predicción:
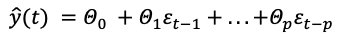
Para obtener los coeficientes, estos errores han de ser expresados en función de los datos de la serie, lo cual suele resultar en expresiones complicadas de minimizar que se han de tratar con métodos especiales.
Modelos ARIMA
Consideremos la diferencia de la serie temporal. Para ello, restamos a la propia serie y(t) la serie desplazada hacia el momento justo anterior. Suponiendo que la diferencia temporal entre muestras temporales de la serie es una unidad, podemos deducir que:
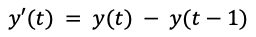
Esta diferencia tiene la propiedad de hacer que las series temporales exhiban un comportamiento más estacionario, que no dependa del tiempo, lo cual se suele prestar mejor a la aplicación de modelos autorregresivos y de media móvil. Los modelos ARIMA son una combinación de los modelos autorregresivos (AR) y los de moving average (MA), aplicados o bien a esta diferencia y', sucesivas diferencias y'', y'''..., o bien a la serie original y:
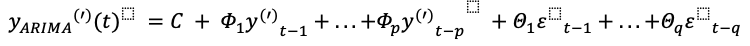
Estos modelos se pueden encontrar en la librería statsmodels de Python. La ventaja de ellos radica en que no necesitan más asunciones que los propios datos y tienen una expresión sencilla. Aunque se prestan también al modelado de estacionalidades, identificar el tipo de modelo ARIMA (el orden AR o MA que usar, el diferenciado…), puede llegar a ser bastante laborioso, y otros modelos como Prophet ofrecen resultados igual o más potentes con menos trabajo y partiendo de hipótesis razonables.
Prophet
Prophet es un programa creado por científicos de Facebook para la predicción de series temporales. Para una guía de cómo utilizar, échale un vistazo a este enlace, y para profundizar véase este artículo. Prophet sigue una descomposición en tendencia y estacionalidades, con la particularidad de que se le pueden añadir días festivos y regresores externos como temperatura:
- La tendencia está modelada por una función continua que es una recta a trozos y que cambia de pendiente en un número de puntos. Se puede poner también un término de saturación para que la tendencia no crezca indefinidamente.
- Las estacionalidades están constituidas por series de Fourier de un determinado orden, controlado por el usuario.
- Los días festivos tienen su propia contribución, que es no nula en una ventana especificada en torno al festivo.
- Los regresores externos son otras series temporales correlacionadas con nuestra serie que pueden ayudar a predecir nuestra serie temporal. Por ejemplo, si queremos saber el número de abrigos vendidos, esperamos que esto tenga una anticorrelación con la temperatura.
De este modo, el modelo de Prophet se puede escribir como:
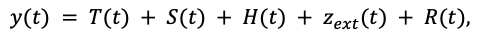
Donde T es la curva variable de tendencia,, H la influencia de los festivos y R es el error restante. En cuanto a los términos que faltan, S es la suma de todas las estacionalidades con distinto período τi:
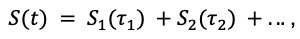
Donde cada Si(τi) es una serie de Fourier. El término del regresor externo es una constante multiplicada por la serie temporal del regresor externo:
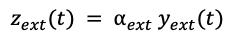
El razonamiento para series multiplicativas es análogo, cambiando las sumas por multiplicaciones. Prophet además permite elegir qué componentes son aditivas y cuáles multiplicativas. Por ejemplo, se puede hacer una tendencia aditiva, una estacionalidad aditiva y otra multiplicativa y festivos aditivos.
Para obtener los parámetros del modelo, Prophet usa inferencia bayesiana. La idea de este método es usar el teorema de Bayes para, a partir de unas distribuciones de partida de los parámetros y los datos obtenidos, saber cuáles son los parámetros más probables que darían lugar a nuestra serie temporal.
Prophet tiene la ventaja de ser muy flexible, potente y fácil de usar. Además, debido a su forma matemática, no necesita que las series sean regulares.
10/03/22 Forecast, machine learning, Prophet



